Giá trị hiện tại của dòng tiền là gì? công thức và ví dụ
Giá trị hiện tại của dòng tiền là khái niệm mà bất kỳ một chuyên gia tài chính hay chỉ là một người quan tâm đến lĩnh vực đầu tư kinh doanh luôn nắm vững vì tầm quan trọng không thể phủ nhận của nó. Đây cũng chính là một trong những khái niệm “nhập môn” vì là nguồn cội tạo ra được những giá trị ước tính tương lai.

Hãy đến với bài viết dưới đây của Isinhvien để nắm rõ định nghĩa và công thức của giá trị hiện tại của dòng tiền nhé.
Giá trị hiện tại của dòng tiền là gì?
Giá trị hiện tại của Dòng tiền (Present Value of Money) chính là giá trị nội tại của dòng tiền sẽ nhận được trong tương lai. Đây là số tiền đại diện cho biết rằng giá trị dòng tiền trong tương lai tương ứng bạn nhận được vào thời điểm hiện tại.
Rõ ràng, giá trị hiện tại của dòng tiền tương lai thấp hơn dòng tiền tương lai theo nghĩa tuyệt đối vì nó dựa trên khái niệm giá trị thời gian của tiền. Theo khái niệm giá trị thời gian của tiền, tiền nhận được ngày hôm nay sẽ có giá trị cao hơn so với tiền nhận được trong tương lai vì tiền nhận được ngày hôm nay có thể được tái đầu tư để kiếm lãi trên nó. Ngoài ra, tiền nhận được ngày hôm nay làm giảm mọi rủi ro bất trắc . Nói tóm lại, thời gian nhận tiền càng lâu thì giá trị hiện tại của nó càng thấp.
Khái niệm giá trị hiện tại rất hữu ích để đưa ra quyết định dựa trên các kỹ thuật lập ngân sách vốn hoặc để đạt được mức định giá chính xác cho một khoản đầu tư. Do đó, điều quan trọng đối với những người tham gia vào việc ra quyết định dựa trên ngân sách vốn, tính toán định giá các khoản đầu tư, công ty..
Công thức tính giá trị hiện tại và ví dụ minh họa
Công thức hệ số giá trị hiện tại:
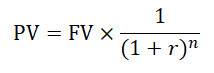
- PV = Giá trị hiện tại
- FV = Giá trị tương lai
- r = Tỷ suất lợi nhuận
- n = Số Năm / Khoảng thời gian
Công thức giá trị hiện tại của dòng tiền được sử dụng để tính giá trị hiện tại của tất cả giá trị tương lai sẽ nhận được. Nó hoạt động dựa trên khái niệm giá trị thời gian tiền bạc. Giá trị thời gian của tiền là khái niệm cho biết một số tiền nhận được ngày hôm nay có giá trị hơn số tiền tương tự nhận được vào một ngày trong tương lai.
Ví dụ về công thức hệ số giá trị hiện tại
Công ty Z đã bán hàng cho Công ty M với giá 5 tỷ đồng. Công ty M đã đưa ra một đề nghị cho Công ty Z rằng một trong hai Công ty M trả 5 tỷ đồng ngay lập tức hoặc trả 5,5 tỷ đổng sau hai năm. Tỷ lệ chiết khấu là 8%.
Bây giờ, để hiểu thỏa thuận nào tốt hơn, tức là liệu Công ty Z có nên lấy 5 tỷ đồng hôm nay hay 5,5 tỷ đồng sau hai năm, chúng ta cần tính giá trị hiện tại của 5,5 tỷ đồng trên lãi suất hiện tại và sau đó so sánh nó với 5 tỷ đồng
Nếu giá trị hiện tại của 5,5 tỷ đồng cao hơn 5 tỷ đồng hiện tại, thì tốt hơn là Công ty Z nên lấy tiền sau hai năm và ngược lại
PV = FV * [1 / (1 + r) n = 5,5 tỷ đồng * [1 / (1 + 8%) 2 ] = 4,715 tỷ đồng
Theo giá trị hiện tại của 5,5 tỷ đồng sau hai năm thấp hơn 5 tỷ đồng, tốt hơn là Công ty Z nên lấy 5 tỷ hôm nay.
Lời kết
Giá trị hiện tại cũng hoạt động như một cơ sở cho các công thức phức tạp khác để đưa ra quyết định phức tạp hơn như tỷ lệ hoàn vốn nội bộ, hoàn vốn chiết khấu, giá trị hiện tại ròng , v.v. Nó cũng hữu ích trong cuộc sống hàng ngày của một người, chẳng hạn như hiểu giá trị hiện tại của EMI cho vay mua nhà hoặc giá trị hiện tại của khoản đầu tư hoàn vốn cố định, v.v.
Trên đây là những thông tin cơ bản về giá trị hiện tại của dòng tiền, độc giả có thể truy cập chuyên mục Kế toán tài chính của Isinhvien để tìm hiểu nhiều nội dung hơn nữa nhé.









