Hướng dẫn phân tích hồi quy tuyến tính đơn giản trong SPSS
Bạn chưa biết cách phân tích hồi quy tuyến tính đơn giản trong SPSS? Mời bạn đọc ngay bài viết dưới đây, Isinhvien đã nêu ví dụ cụ thể kèm hướng dẫn chi tiết cách thực hiện. Nhớ theo dõi nhé!
Phân tích hồi quy tuyến tính đơn giản trong SPSS
Định nghĩa phân tích hồi quy tuyến tính đơn giản
Phân tích hồi quy tuyến tính đơn giản (Simple Linear Regression Analysis) là
tìm sự liên hệ giữa 2 biến số liên tục: biến độc lập (biến dự đoán) trên trục hoành x
với biến phụ thuộc (biến kết cục) trên trục tung y. Sau đó vẽ một đường thẳng hồi
qui và từ phương trình đường thẳng này ta có thể dự đoán được biến y (ví dụ: cân
nặng) khi đã có x (ví dụ: tuổi)
Hướng dẫn thực hành phân tích hồi quy tuyến tính đơn giản trong SPSS
Ví dụ: Ta có 1 mẫu gồm 6 trẻ em khác có cân nặng theo bảng sau:
| Tuổi | Cân nặng (Kg) |
| 1 | 11 |
| 2 | 11 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | 20 |
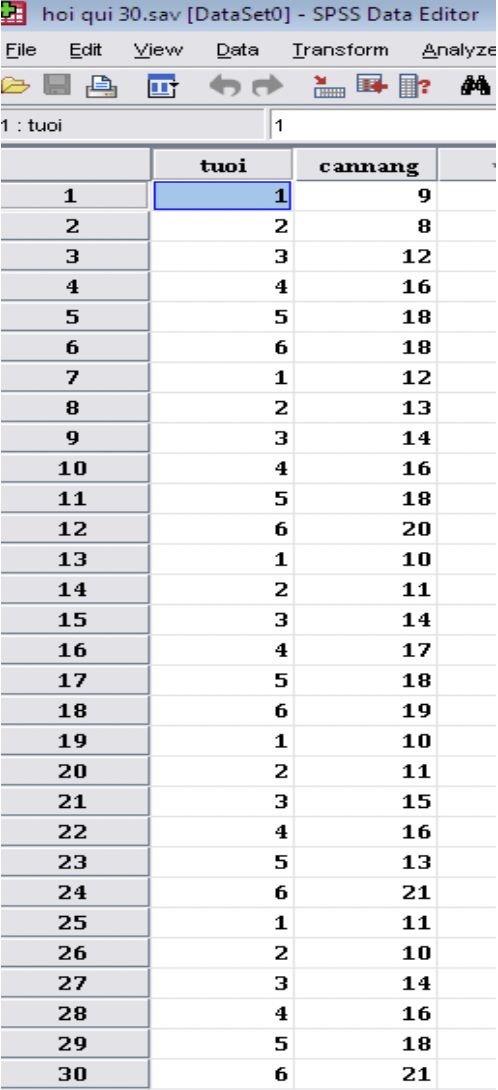
Nhập số liệu tuổi và cân nặng cân được của 30 trẻ 1-6 tuổi vào SPSS:
Cột 1: tuổi; cột 2: cân nặng
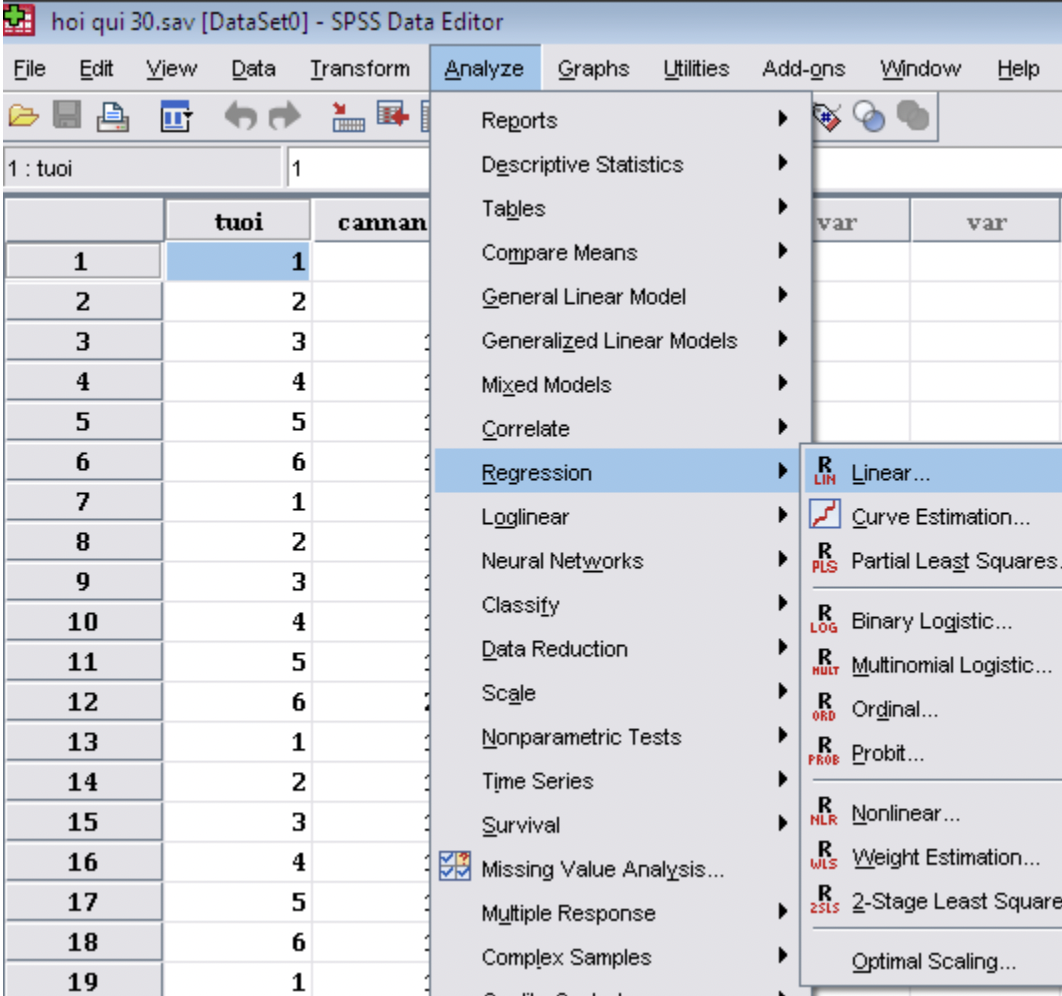
Vào menu: >Analyze> Regression> Linear

Hệ số tương quan R=0,918 và R2 (R bình phương) = 0,843
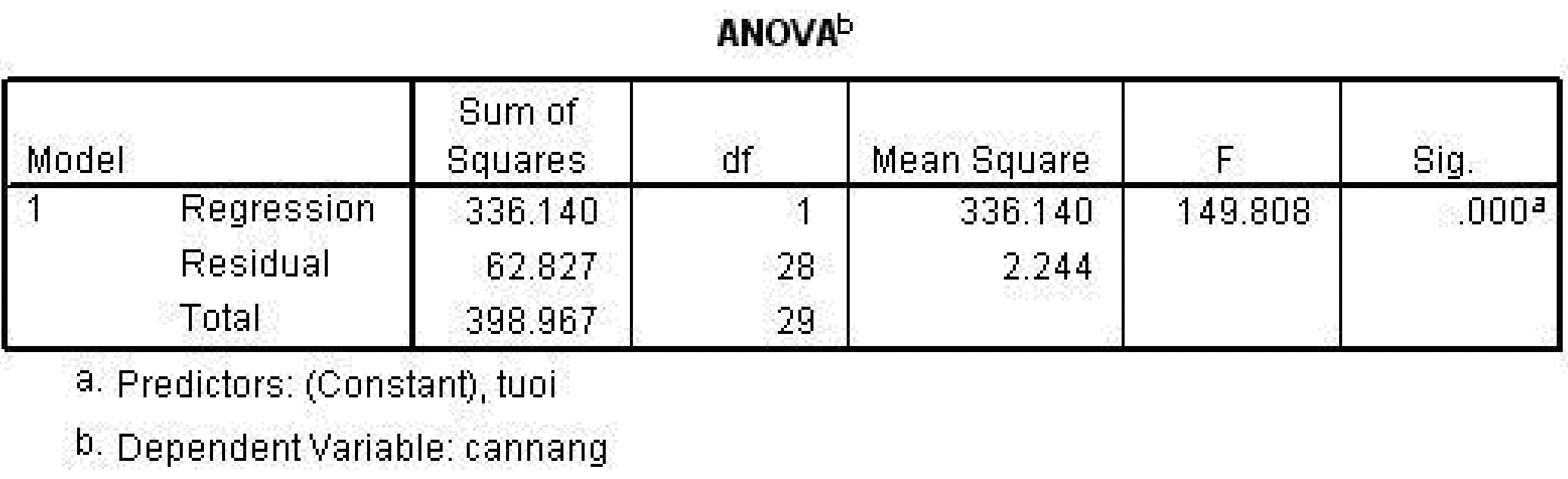
Tổng bình phương phần hồi qui (Regression)=336,14
Tổng bình phương phần dư (Residual)=62,8
Trung bình bình phương hồi qui: 336,14/ 1 (bậc tự do)=336,14
Trung bình bình phương phần dư: 62,8/ 28(bậc tự do=n-2)=2,24
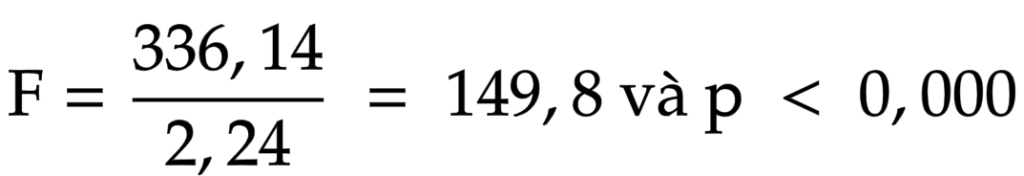
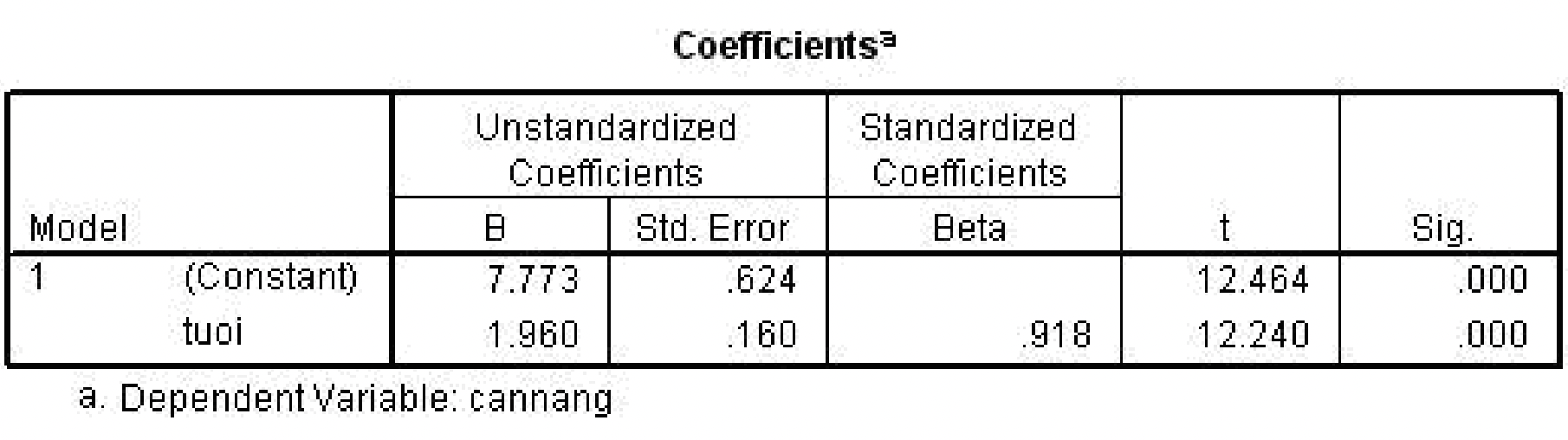
Kết quả bảng 3 cho biết hệ số tương quan Beta (độ dốc) = 1,96 và điểm cắt tại trung
tung là Alpha =7.773
Phương trình đường thẳng hồi qui được viết:
Cân nặng= 7,77 + 1,96 x tuổi
Như vậy khi em bé tăng lên 1 tuổi thì cân nặng tăng lên 1,96 kg
Vẽ đường thẳng hồi qui trong SPSS
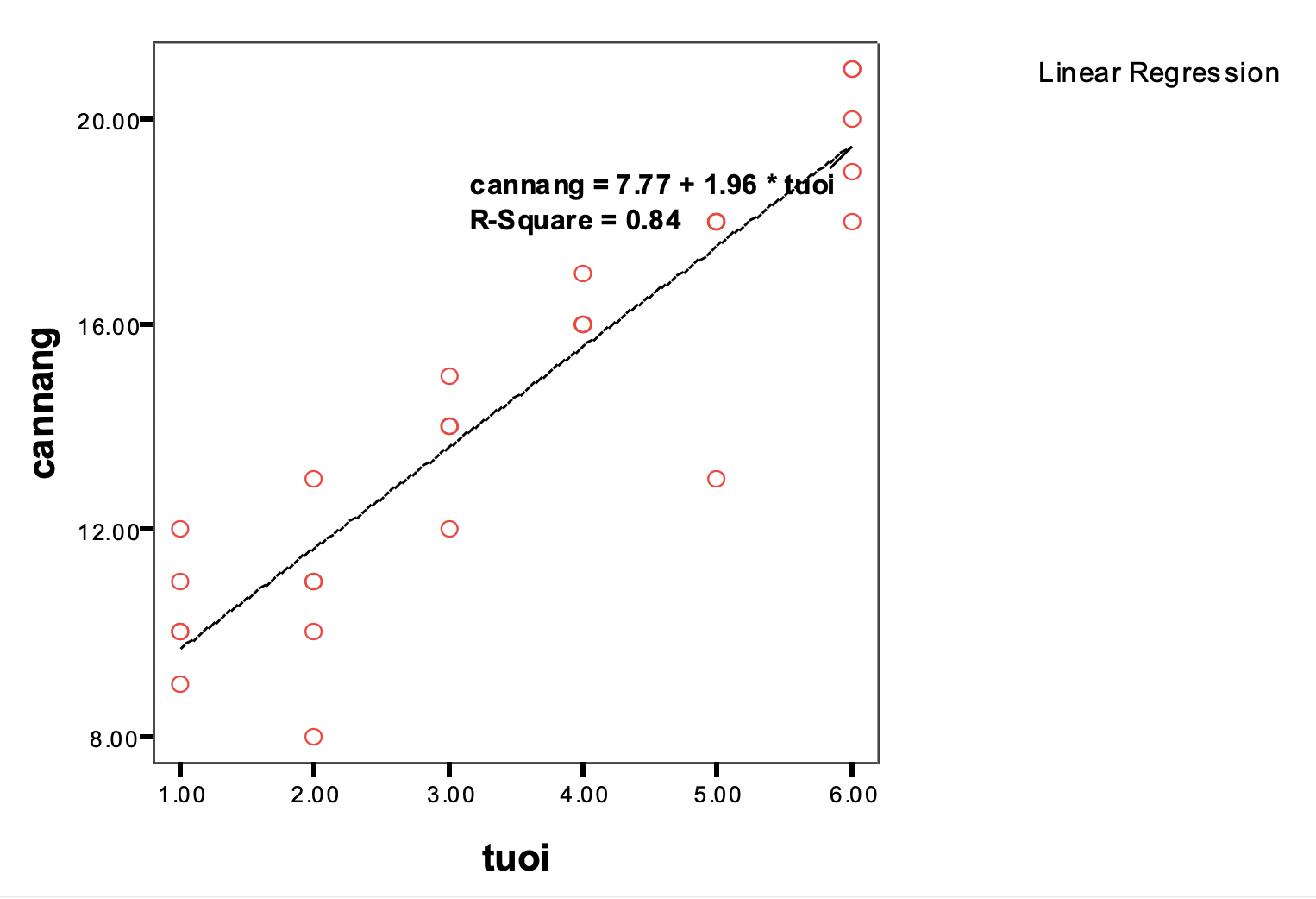
Từ phương trình này ta có thể ước đoán được cân nặng theo tuổi của trẻ, tuy nhiên
nằm trong một giới hạn nào đó chẳng hạn như từ 1-12 tuổi, vì sau tuổi này cân nặng
trẻ sẽ tăng vọt trong thời kỳ dậy thì và không còn liên hệ tuyến tính với tuổi nữa.
Ví dụ muốn ước đoán cân nặng của trẻ từ quần thể nghiên cứu này:
7 tuổi => Cân nặng = 7,77 + 1,96 x7 = 21,49 kg
8 tuổi => Cân nặng= 7,77 + 1,96 x8 = 23,45 kg
>> Hướng dẫn phân tích hồi quy đa biến trong SPSS dễ hiểu nhất
Các giả định trong phân tích hồi qui tuyến tính
Phân tích hồi qui tuyến tính không chỉ là việc mô tả các dữ liệu quan sát
được trong mẫu (sample) nghiên cứu mà cần phải suy rộng cho mối liên hệ
trong dân số (population).
Vì vậy, trước khi trình bày và diễn dịch mô hình hồi
qui tuyến tính cần phải dò tìm vi phạm các giả định. Nếu các giả định bị vi
phạm thì các kết quả ước lượng không đáng tin cậy được.
Các giả định cần thiết trong hồi qui tuyến tính:
- xi là biến số cố định, không có sai sót ngẫu nhiên trong đo lường.
- Phần dư (trị số quan sát trừ cho trị số ước đoán) phân phối theo luật
phân phối chuẩn - Phần dư có trị trung bình bằng 0 và phương sai không thay đổi cho mọi
trị xi - Không có tương quan giữa các phần dư
Hi vọng với bài viết hướng dẫn phân tích hồi quy tuyến tính đơn giản trong SPSS trên đây của Isinhvien sẽ giúp bạn hiểu và thực hành tốt. Nếu thấy hữu ích thì nhớ Like, Comment và Share bài này nhé. Chúc bạn học tốt!
Bài viết khác liên quan đến Kinh tế lượng
- Kinh tế lượng – Giáo trình – Bài tập (có đáp án) và đề thi tham khảo
- SPSS là gì? Ứng dụng và chức năng cốt lõi của SPSS trong nghiên cứu khoa học
- Hướng dẫn phân tích hồi quy đa biến trong SPSS dễ hiểu nhất